DS dérivées
dérivées - DS2H
Ce DS comporte trois exercices :
exo 1 : calculer f '(x) pour six expressions de f(x)
corrigé 1
exo 2 : On donne la représentation graphique Cf d'une fonction rationnelle f et un point A n'appartenant pas à Cf . On demande :
1) de calculer f'(x)
2) de déterminer les droites tangentes à Cf parallèles à l'axe (Ox)
3) de déterminer les droites tangentes à Cf passant par A .
corrigé 2
exo 3 : On définit f(x) en utilisant les notions de valeur absolue et de racine carrée . On demande :
1) de déterminer l'ensemble de définition de f puis d'écrire f(x) sans le symbole de la valeur absolue
2) de faire une étude de dérivabilité à droite de -4
3) de faire une étude de dérivabilité en 0
4) de calculer f '(x) quand c'est possible
5) de déterminer les droites tangentes à Cf parallèles à l'axe (Ox)
6) d'écrire une équation d'une droite tangente à Cf puis de la tracer
corrigé 3
dérivées - DS4H
Ce DS comporte cinq exercices
exo 1 : un QCM
corrigé 1
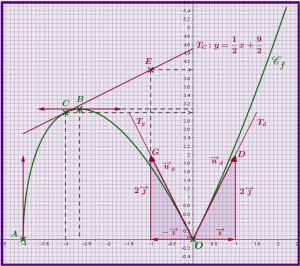
exo 2 : On donne la représentation graphique Cf d'une fonction rationnelle ( degré 3 /degré 2) . On demande :
1) d'étudier les limites de f aux bornes de Df
2) d'écrire autrement f(x) puis d'en déduire l'existence d'une droite ? asymptote oblique pour Cf
3) de calculer f '(x) quand c'est possible puis de rechercher des droites tangentes parallèles à l'axe (Ox) , des droites tangentes parallèles à ? , des droites tangentes passant par un point A non situé sur Cf
corrigé 2
exo 3 : On demande de calculer f '(x) pour huit expressions de f(x)
corrigé 3
exo 4 : Cet exercice se résoud de manière graphique . On donne la représentation graphique Cf d'une fonction avec des droites tangentes à Cf , des demi-tangentes à Cf . On demande :
1) de lire des nombres dérivés
2) de donner la valeur de limite associées à la notion de nombre dérivé
3) de faire une étude de dérivabilité
corrigé 4

exo 5 : On donne f(x) ( en utilisant une racine carrée et un monôme du second degré ) et la représentation graphique Cf de f . On demande :
1) de justifier que f est définie en tout réel positif puis de faire une étude de dérivabilité de f en 0
2) de calculer f'(x) quand c'est possible
3) d'écrire l'équation réduite de la droite T tangente à Cf en son point d'abscisse 1
4) d'étudier la position relative de Cf par rapport à T en utilisant le tableau de variation d'une fonction auxiliaire .
corrigé 5